这是本系列的第二篇文章,先把成果放上去啦
注意,本项目是“C”项目,不是“ C++ ”项目,选择新建项目需要选择“C Project”,代码文件确保以”.c”结尾,否则无法正常运行
放到云平台上的BUG
由于云平台是Linux系统,没法直接引入<math.h>文件,所以直接运行我的代码会出问题。
所以在运行之前,需要改一下设置,具体设置方法如下:
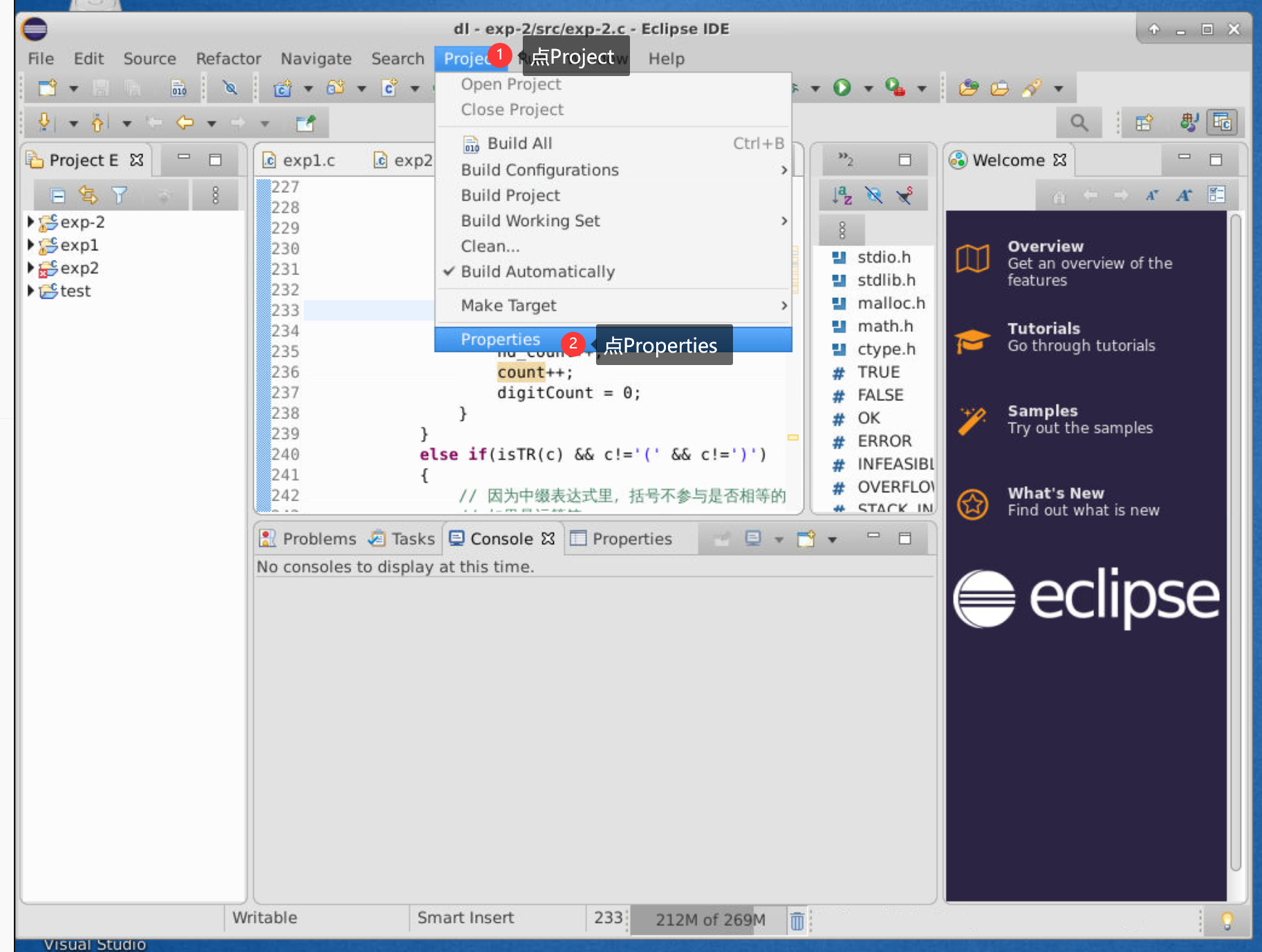
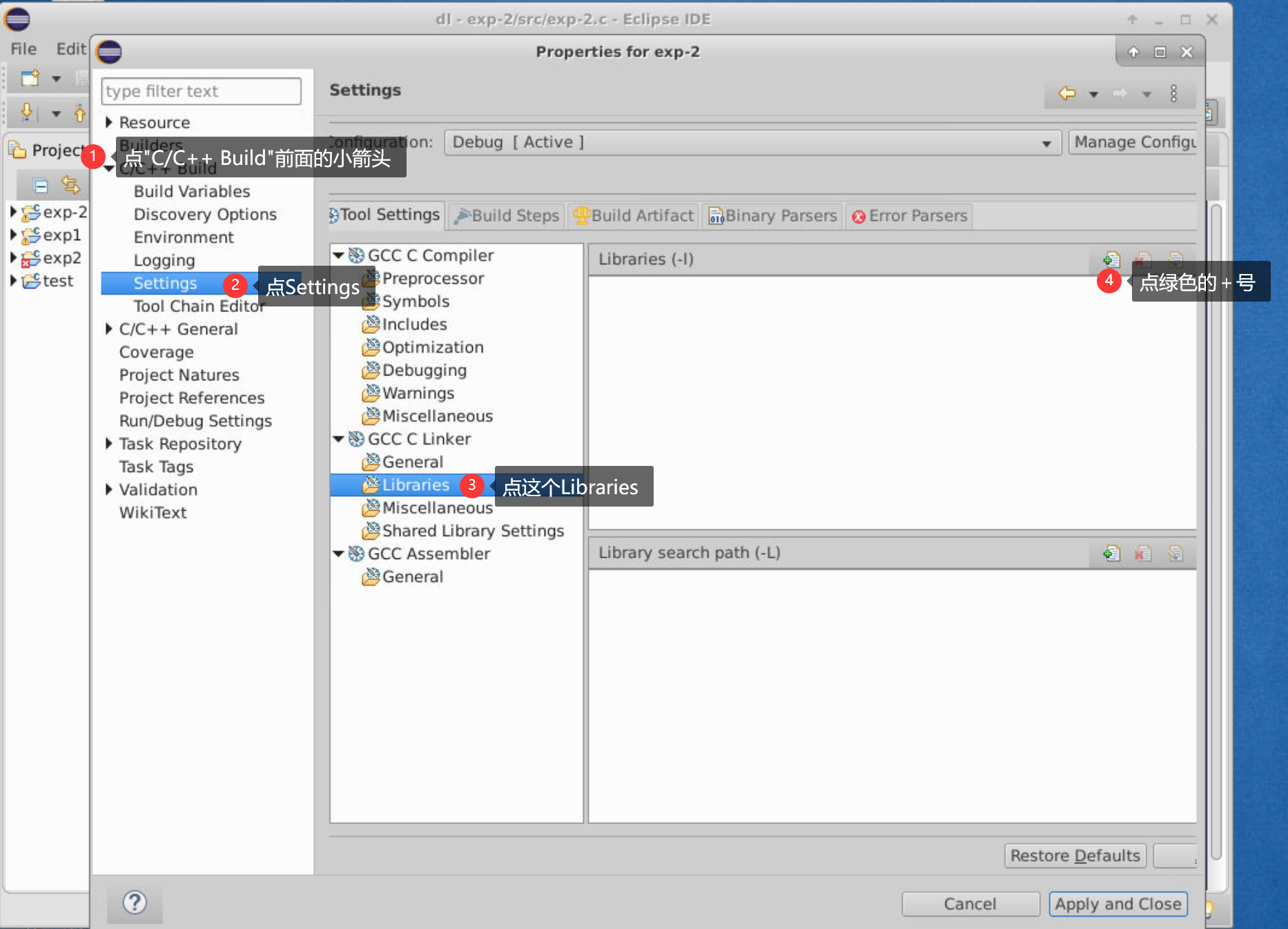
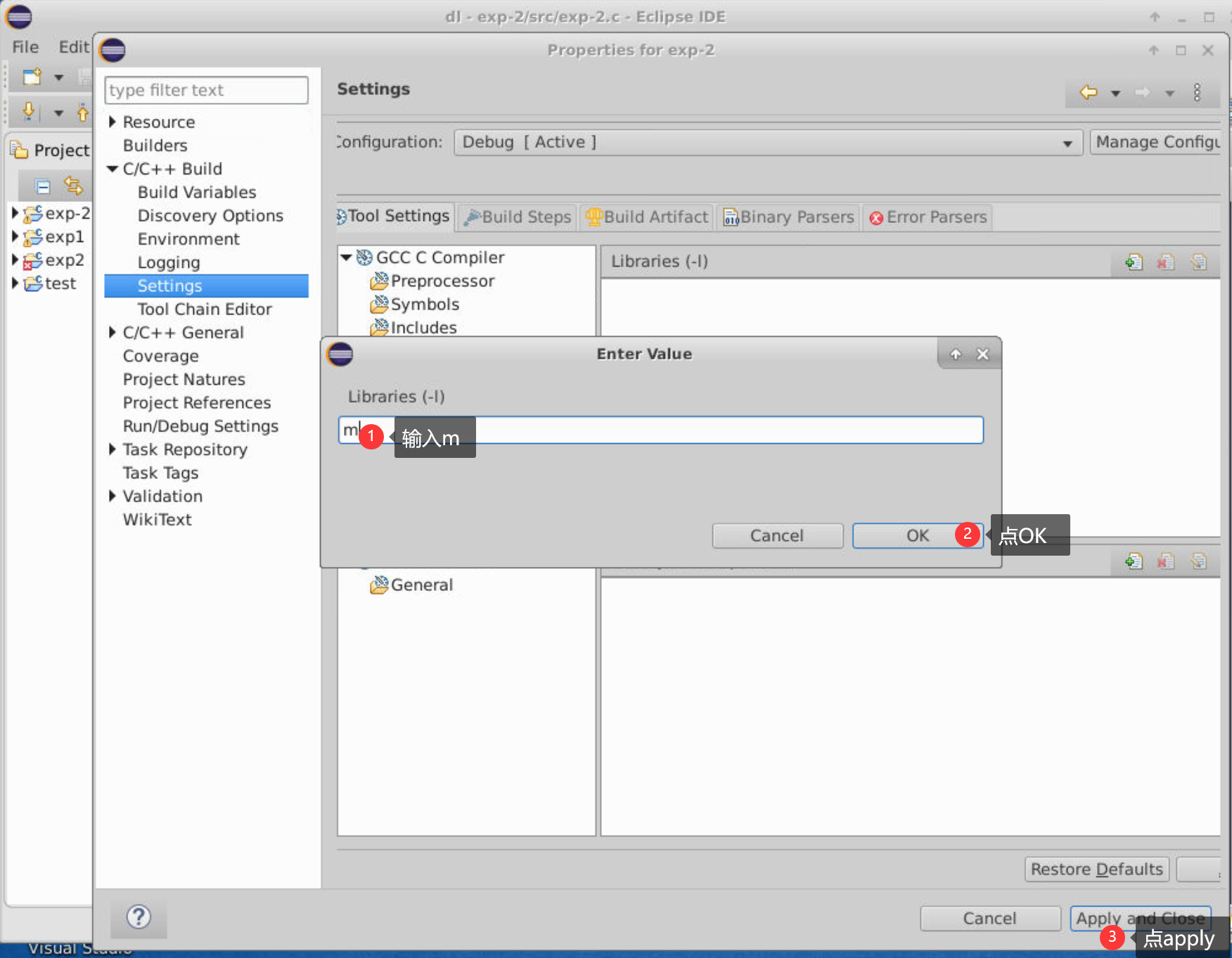
然后应该就可以了,如果还不行,就直接滴滴我吧
题目描述
栈是一种很重要的数据结构,具有“后进先出”的特点。为了提高对栈的掌握和运用水平,本实验构建栈来分别计算波兰式、逆波兰式和中缀表达式的结果。
源代码
代码略长,有大约700行,比第一个实验要多一倍。
#include <stdio.h>
#include <stdlib.h>
#include <malloc.h>
#include <math.h>
#include <string.h>
#include <ctype.h>
#define TRUE 1
#define FALSE 0
#define OK 1
#define ERROR 0
#define INFEASIBLE -1
#define OVERFLOW -2
#define STACK_INIT_SIZE 100
#define STACKINCREMENT 10
#define MAXINPUT 1000
typedef int status;
typedef struct optrStack {
char *base;
char *top;
int stacksize;
} optrStack;
typedef struct opndStack {
int *base;
int *top;
int stacksize;
} opndStack;
void intro();
int menu();
status initTR(optrStack *stack);
status initND(opndStack *stack);
char getTopTR(optrStack stack);
int getTopND(opndStack stack);
status getInput(char *exp, int mode);
int isError(char *exp, int mode);
status pushTR(optrStack *stack, char e);
status pushND(opndStack *stack, int e);
status popTR(optrStack *stack, char *e);
status popND(opndStack *stack, int *e);
int isND(char c);
int isTR(char c);
int operate(int a, char theta, int b);
char precede(char a, char b);
status calcPolan();
status calcNPolan();
status calcMiddle();
int char2int(char c);
int str2int(char *s, int count, int digitCount);
int str2intTraverse(char *s, int count, int digitCount);
int main() {
// 介绍功能
intro();
// 定义变量
int select;
do {
// 获取用户输入
select = menu();
// 根据输入来选择功能
switch (select) {
case 1:
calcPolan();
break;
case 2:
calcNPolan();
break;
case 3:
calcMiddle();
break;
default:
printf("谢谢使用,再见!\n");
break;
}
} while (select != 4);
return 0;
}
void intro() {
// 本函数用于展示程序一开始的页面,以及使用说明
printf("**********************************\n");
printf("* *\n");
printf("* 计算表达式运算器 *\n");
printf("* *\n");
printf("**********************************\n\n");
printf("本运算器可以实现波兰式计算、逆波兰式计算、中缀表达式计算\n");
printf("\n\n");
}
int menu() {
// 用于展示菜单
printf("\n请选择需要进行计算的表达式:\n");
printf("1\t波兰式\n");
printf("2\t逆波兰式\n");
printf("3\t中缀表达式\n");
printf("4\t退出系统\n");
printf("请输入您想做的功能的序号,并按回车键:\n");
// 获取输入
int select;
scanf("%d", &select);
// 虽然这个看起来微不足道,但是他确实给我造成了很大的困扰
// 如果不加getchar()的话,输入的最后一个字符就会被传送到后面的输入里去
// 比如回车,就会被传过去,造成下面的gets()函数挂掉
getchar();
return select;
}
int isError(char *exp, int mode) {
// 用于检验输入的字符串是否有问题
int result = 0;
int count = 0;
int left_bracket_count = 0;
int right_bracket_count = 0;
int tr_count = 0;
int nd_count = 0;
char c;
int digitCount = 0;
// 通用的情况
while (exp[count] != '\0') {
// 验证是否为非法输入
char c = exp[count];
if (!isTR(c) && !isND(c) && c != ' ') {
result = 1;
printf("存在非法字符,请重新输入\n");
return result;
}
// 查看括号是否匹配——保证左括号在前,右括号在后
if (c == '(')
left_bracket_count++;
if (c == ')')
right_bracket_count++;
if (right_bracket_count > left_bracket_count) {
result = 1;
printf("保证左括号在前,右括号在后,请重新输入\n");
return result;
}
if (exp[count + 1] == ' ' || exp[count + 1] == '\0') {
count++;
continue;
}
// 主要验证一下,同一个“段”内,是不是都是数字或者符号
while (exp[count + 1] != ' ' && exp[count + 1] != '\0') {
// 如果下一个是空格,那就说明应该要断了
// 但是如果不是,那么就说明是有两位以上的数字
// 或者输入错误,即数字和运算符放一块了,就要重新输入
// 首先看是不是运算符,如果是,那肯定就是输入错了
if (isTR(exp[count])) {
// 运算符只能单独成一段,后面还不是空格,必是错的
printf("运算符前后必须有空格,请重新输入:\n");
result = 1;
return result;
}
if (isND(exp[count])) {
// 如果第一个是数字,那么后面接的必须也是数字
if (!isND(exp[count + 1])) {
result = 1;
printf("数字与字符不得在同一节内混输,请重新输入:\n");
return result;
}
}
count++;
}
// 如果输入有问题,就跳出去准备重新输入
if (result) {
return result;
}
}
// 最后要看一下左右括号数量是否相等
if (left_bracket_count != right_bracket_count) {
result = 1;
printf("左右括号数量不相等,请重新输入:\n");
return result;
}
// 验证操作数和运算符数目不匹配的情况
if (mode == 1 || mode == 2 || mode == 3) {
// 开始操作
count = 0;
while (exp[count] != '\0') {
c = exp[count];
// 统计ND和TR的数量,——直接把下面的拿来魔改
if (isND(c)) {
if (exp[count + 1] == ' ' || exp[count + 1] == '\0') {
// 说明就是一位数字,直接入栈就行(入的int数字)
nd_count++;
count++;
} else {
// 但多位数字的情况,比如124就要占三个字符
// 所以要用个循环看一下
while (exp[count + 1] != ' ' && exp[count + 1] != '\0') {
// 那说明是一个多位数字了
digitCount++;
count++;
}
nd_count++;
count++;
digitCount = 0;
}
} else if (isTR(c) && c != '(' && c != ')') {
// 因为中缀表达式里,括号不参与是否相等的验证。
// 如果是运算符
tr_count++;
count++;
} else if (c == ' ' || c == '(' || c == ')') {
// 取到了空格,走下一个
count++;
} else {
// 特殊情况
printf("有一个字符既不是操作数又不是操作符,自动跳过\n");
count++;
}
}
// 统计完毕后,如果数量相差不是1,那就说明有问题
if (nd_count - tr_count != 1) {
result = 1;
printf("操作数和运算符数目不匹配,请重新输入:\n");
return result;
}
}
return result;
}
status getInput(char *exp, int mode) {
// 用于获得用户输入,并做一些基础的验证处理
gets(exp);
while (isError(exp, mode)) {
printf("请重新输入:\n");
gets(exp);
}
return OK;
}
int char2int(char c) {
// 用于把单个字符转成数字
return c - 48;
}
int str2int(char *s, int count, int digitCount) {
// 把多个字符转成一个多位数字
int result = 0;
int i, digit;
for (i = digitCount - 1; i >= 0; i--) {
digit = char2int(s[count - i]);
result += digit * pow(10, i);
}
return result;
}
int str2intTraverse(char *s, int count, int digitCount) {
// 把多个字符变成一个多位数字的 逆序版本
int result = 0;
int i, digit;
for (i = 0; i < digitCount; i++) {
digit = char2int(s[count + i]);
result += digit * pow(10, digitCount - i - 1);
}
return result;
}
int isND(char c) {
// 判断一个字符是不是操作数
// 其实直接用isdigit就行了,但是为了保持对称,还是用isND
return isdigit(c);
}
int isTR(char c) {
// 判断一个字符是不是操作符
char trSet[] = {'+', '-', '*', '/', '(', ')', '\0'};
int flag = 0;
for (int i = 0; i < 7; i++) {
if (c == trSet[i]) {
flag = 1;
}
}
return flag;
}
int operate(int a, char theta, int b) {
// 用于计算三元表达式结果
switch (theta) {
case '+':
return a + b;
case '-':
return a - b;
case '*':
return a * b;
case '/':
return a / b;
default:
return ERROR;
}
}
char precede(char a, char b) {
// 判断两个字符的优先级
char big = '>';
char small = '<';
char same = '=';
switch (a) {
case '+':
if (b == '*' || b == '/' || b == '(')
return small;
else
return big;
break;
case '-':
if (b == '*' || b == '/' || b == '(')
return small;
else
return big;
break;
case '*':
if (b == '(')
return small;
else
return big;
break;
case '/':
if (b == '(')
return small;
else
return big;
break;
case '(':
if (b == ')')
return same;
else
return small;
break;
case ')':
return big;
break;
case '\0':
if (b == '\0')
return same;
else
return small;
default:
return same;
}
}
status calcPolan() {
// 计算波兰式
// 获得用户输入,假设用户输入的字符小于MAXINPUT个
char PolanExp[MAXINPUT];
printf("\n请输入波兰式表达式,例如+ 2 * 3 - 5 1(中间需要有空格):\n");
getInput(PolanExp, 1);
// 初始化栈
// 在这里只要用到一个数字栈
opndStack opnd;
initND(&opnd);
// 对所获得的字符串进行处理
int count = 0;
int digitCount = 1;
char x, theta;
int a, b;
// 使用string.h里面的strlen函数(不考虑结尾'\0'字符)
int length = strlen(PolanExp);
for (count = length; count >= 0;) {
// 这里的处理方式跟别的有些不同,因为是倒序处理的
// 所以这里的各种++就都要改为--
// 取出要处理的字符
char c = PolanExp[count];
// 如果是操作数,入栈
if (isND(c)) {
// 由于这里可能会出现数组下溢的情况,所以就要先判断一下
if (count == 0) {
// c是nd并且是最后一位,那肯定是一位数字,直接入栈
pushND(&opnd, char2int(c));
count--;
} else {
// 现在就可以来判断是否是多位数字了
if (PolanExp[count - 1] == ' ') {
// 说明就是一位数字,直接入栈就行(入的int数字)
pushND(&opnd, char2int(c));
count--;
} else {
// 但多位数字的情况,比如124就要占三个字符
// 所以要用个循环看一下
while (PolanExp[count - 1] != ' ') {
// 那说明是一个多位数字了
digitCount++;
count--;
}
int multiDigitInt = str2intTraverse(PolanExp, count, digitCount);
pushND(&opnd, multiDigitInt);
digitCount = 0;
count--;
}
}
} else if (isTR(c)) {
// 如果是运算符进来了,直接进行运算
popND(&opnd, &a);
popND(&opnd, &b);
theta = c;
pushND(&opnd, operate(a, theta, b));
count--;
} else if (c == ' ') {
// 取到了空格,走下一个
count--;
} else {
// 特殊情况
printf("有一个字符既不是操作数又不是操作符,自动跳过\n");
count--;
}
}
printf("\n波兰式计算结果为:\n%s = %d\n\n", PolanExp, getTopND(opnd));
return OK;
}
status calcNPolan() {
// 计算逆波兰式
// 获得用户输入,假设用户输入的字符小于MAXINPUT个
char NPolanExp[MAXINPUT];
printf("\n请输入逆波兰式表达式,例如2 3 5 1 - * +(中间需要有空格):\n");
getInput(NPolanExp, 2);
// 初始化栈
// 在这里只要用到一个数字栈
opndStack opnd;
initND(&opnd);
// 对所获得的字符串进行处理
int count = 0;
int digitCount = 1;
char x, theta;
int a, b;
// 开始处理字符串——这里就不用考虑最后一个\0符号了
while (NPolanExp[count] != '\0') {
// 取出要处理的字符
char c = NPolanExp[count];
// 如果是操作数,入栈
if (isND(c)) {
if (NPolanExp[count + 1] == ' ' || NPolanExp[count + 1] == '\0') {
// 说明就是一位数字,直接入栈就行(入的int数字)
pushND(&opnd, char2int(c));
count++;
} else {
// 但多位数字的情况,比如124就要占三个字符
// 所以要用个循环看一下
while (NPolanExp[count + 1] != ' ' && NPolanExp[count + 1] != '\0') {
// 那说明是一个多位数字了
digitCount++;
count++;
}
int multiDigitInt = str2int(NPolanExp, count, digitCount);
pushND(&opnd, multiDigitInt);
count++;
digitCount = 0;
}
} else if (isTR(c)) {
// 如果是运算符进来了,直接进行运算
popND(&opnd, &b);
popND(&opnd, &a);
theta = c;
pushND(&opnd, operate(a, theta, b));
count++;
} else if (c == ' ') {
// 取到了空格,走下一个
count++;
} else {
// 特殊情况
printf("有一个字符既不是操作数又不是操作符,自动跳过\n");
count++;
}
}
printf("\n逆波兰式计算结果为:\n%s = %d\n\n", NPolanExp, getTopND(opnd));
return OK;
}
status calcMiddle() {
// 计算中缀表达式
// 获得用户输入,假设用户输入的字符小于MAXINPUT个
char middleExp[MAXINPUT];
printf("\n请输入中缀表达式,例如4 + 2 * 3 - 10 / 5(中间需要有空格):\n");
getInput(middleExp, 3);
// 初始化栈
optrStack optr;
opndStack opnd;
initTR(&optr);
initND(&opnd);
// 在运算符栈里面放一个开始的标志
pushTR(&optr, '\0');
// 对所获得的字符串进行处理
int count = 0;
int digitCount = 1;
char x, theta;
int a, b;
// 使用string.h里面的strlen函数获取字符串长度
int length;
length = strlen(middleExp);
// 因为我们打算把最后一个\0字符也给考虑进来
length++;
for (count = 0; count < length;) {
// 取出要处理的字符
char c = middleExp[count];
// 如果是操作数,入栈
if (isND(c)) {
if (middleExp[count + 1] == ' ' || middleExp[count + 1] == '\0') {
// 说明就是一位数字,直接入栈就行(入的int数字)
pushND(&opnd, char2int(c));
count++;
} else {
// 但多位数字的情况,比如124就要占三个字符
// 所以要用个循环看一下
while (middleExp[count + 1] != ' ' && middleExp[count + 1] != '\0') {
// 那说明是一个多位数字了
digitCount++;
count++;
}
int multiDigitInt = str2int(middleExp, count, digitCount);
pushND(&opnd, multiDigitInt);
count++;
digitCount = 1;
}
} else if (isTR(c)) {
// 如果是运算符,则要比较优先级
switch (precede(getTopTR(optr), c)) {
case '<':
// 栈顶元素优先级低
pushTR(&optr, c);
count++;
break;
case '=':
// 脱括号并接收下一个字符
popTR(&optr, &x);
count++;
break;
case '>':
popTR(&optr, &theta);
popND(&opnd, &b);
popND(&opnd, &a);
pushND(&opnd, operate(a, theta, b));
}
} else if (c == ' ') {
// 取到了空格,走下一个
count++;
} else {
// 特殊情况
printf("有一个字符既不是操作数又不是操作符,自动跳过\n");
count++;
}
}
printf("\n中缀表达式计算结果为:\n%s = %d\n\n", middleExp, getTopND(opnd));
return OK;
}
status initTR(optrStack *stack) {
// 初始化一个栈
stack->base = (char *) malloc(STACK_INIT_SIZE * sizeof(char));
if (!stack->base) {
exit(OVERFLOW);
}
stack->top = stack->base;
stack->stacksize = STACK_INIT_SIZE;
return OK;
}
status initND(opndStack *stack) {
// 初始化一个栈
stack->base = (int *) malloc(STACK_INIT_SIZE * sizeof(int));
if (!stack->base) {
exit(OVERFLOW);
}
stack->top = stack->base;
stack->stacksize = STACK_INIT_SIZE;
return OK;
}
char getTopTR(optrStack stack) {
// 取栈顶元素
if (stack.base == stack.top) {
return ERROR;
} else {
return *(stack.top - 1);
}
}
int getTopND(opndStack stack) {
// 取栈顶元素
if (stack.base == stack.top) {
return ERROR;
} else {
return *(stack.top - 1);
}
}
status pushTR(optrStack *stack, char e) {
// 插入元素e为新的栈顶元素
if (stack->top - stack->base >= stack->stacksize) {
// 满了,分配新空间
stack->base = (char *) realloc(stack->base, (stack->stacksize + STACKINCREMENT) * sizeof(char));
if (!stack->base) {
exit(OVERFLOW);
}
stack->top = stack->base + stack->stacksize;
stack->stacksize += STACKINCREMENT;
}
*(stack->top++) = e;
return OK;
}
status pushND(opndStack *stack, int e) {
// 插入元素e为新的栈顶元素
if (stack->top - stack->base >= stack->stacksize) {
// 满了,分配新空间
stack->base = (int *) realloc(stack->base, (stack->stacksize + STACKINCREMENT) * sizeof(int));
if (!stack->base) {
exit(OVERFLOW);
}
stack->top = stack->base + stack->stacksize;
stack->stacksize += STACKINCREMENT;
}
*(stack->top++) = e;
return OK;
}
status popTR(optrStack *stack, char *e) {
// 删除栈元素并用e带回
if (stack->top == stack->base) {
return ERROR;
} else {
*e = *(--(stack->top));
return OK;
}
}
status popND(opndStack *stack, int *e) {
// 删除栈元素并用e带回
if (stack->top == stack->base) {
return ERROR;
} else {
*e = *(--(stack->top));
return OK;
}
}

代码很好 是我的了
打完德扑还能回去卷一手数据结构是我没想到的
实验要求除了求值,好像还要把波兰式和逆波兰转成中缀表达式输出
它在评分标准里面确实是把那俩给转中缀了,但是我琢磨着他可能是给人看的,起码没有明说要转。如果真的要转的话,,我选择放弃这一部分的分数哈哈哈